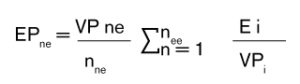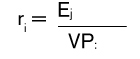El método de la unidad monetaria. El enfoque estándar

Albert Vidal Barberà
Francisco Julián Chico Martínez
Auditores
Sindicatura de Cuentas de Cataluña.

Resumen
Este artículo, basado en la normativa y recomendaciones de la Comisión Europa, desarrolla el método estadístico de la unidad monetaria en su enfoque estándar. Se detalla el procedimiento secuencial que sigue en la aplicación de este método: la determinación del tamaño de la muestra y su selección, la fiscalización y la detección de errores de la muestra, la proyección de los errores a la población, el cálculo de la precisión y la evaluación de los resultados. Se destacan los pros y los contras de este método, comparándolo con otros alternativos. Se explican las principales fórmulas y variables utilizadas y, finalmente, se intenta reforzar los conceptos expuestos mediante un ejemplo práctico y una conclusión. Palabras clave
Selección de muestras, Muestreo de la Unidad Monetaria, intervalo de muestreo, error tolerable, error proyectado, intervalo de confianza.
Abstract
This article, based on the rules and recommendations of the European Commission, develops the statistical method of monetary unit sampling in its standard approach. The sequential procedure followed in the application of this method is detailed: determining the sample size and selection; auditing and detecting errors in the sample; projecting the errors to the whole population; calculating the precision, and evaluating the results. The advantages and disadvantages of this method, as compared to alternative methods, are discussed. The main formulae and variables used are explained and, finally, there is a practical example and a conclusion to help reinforce the concepts presented.
Key Words
Sample selection, Monetary Unit Sampling, cut-off value, tolerable error, projected error, confidence interval

1. INTRODUCCIÓN

La selección de los elementos a fiscalizar para llevar a cabo las pruebas sustantivas y/o de cumplimento es un proceso esencial en toda fiscalización y así lo recogen los diferentes manuales de fiscalización de la mayoría de los Organismos de Control Externo.

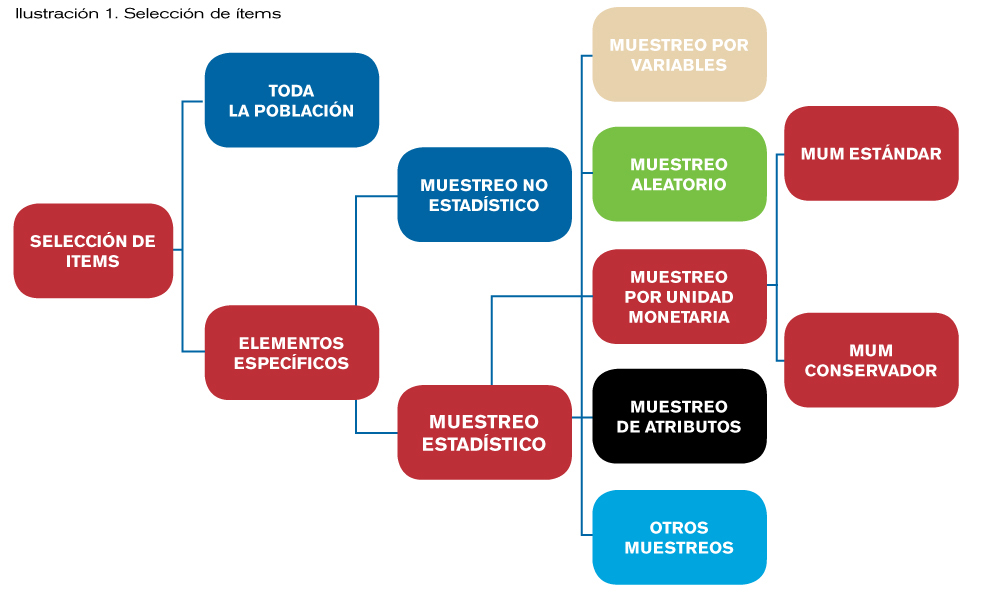
El auditor, en la fase de planificación y/o en la de ejecución del trabajo de campo puede, cuando no selecciona toda la población, escoger entre hacer una selección siguiendo su criterio, realizar un muestreo estadístico o hacer una combinación de las dos opciones anteriores. (Véase la ilustración 1)

En este artículo se desarrollará el Método estadístico de muestreo de la unidad monetaria (en adelante MUM), en su enfoque estándar que, junto con el MUM en su enfoque conservador, es el método estadístico por el cual la Unión Europea manifiesta preferencia en la selección de muestras^[1].

2.EL MÉTODO DE LA UNIDAD MONETARIA. ENFOQUE ESTÁNDAR

El MUM es un método estadístico de selección de muestras que utiliza, como su nombre indica, la unidad monetaria como variable auxiliar para realizar el muestreo y en el cual la probabilidad de que un elemento de la población sea escogido es directamente proporcional a su valor monetario; es decir que los elementos de más valor tienen mayor probabilidad de ser seleccionados que los de menor valor.

Como cualquier otro método estadístico de muestreo, el MUM persigue la representatividad de la muestras y su objetivo final es el de proyectar o extrapolar los errores detectados en la muestra para cuantificar el error total y concluir si la población presenta errores materiales o no.

Sin perjuicio de otras clasificaciones el MUS puede presentar dos enfoques, el enfoque estándar que, entre otras características, parte de la premisa que la población sigue una distribución probabilística Normal y el enfoque conservador, que es el más sencillo, usado y recomendado por la Comisión Europea, que considera que la población sigue la distribución de Poisson.

En este artículo se explica  el enfoque estándar del MUM o MUM estándar, que tiene como principales características las siguientes:

1. Se basa, como ya se ha mencionado, en la hipótesis de que los importes a fiscalizar siguen una distribución probabilística Normal.
2. Se requiere del conocimiento de la varianza de los porcentajes de error de la población para poder establecer el tamaño de la muestra.
3. Es aplicable cuando los elementos de la población presentan errores que no son similares, son proporcionales a los valores de las operaciones y cuando los valores de los elementos de la población presentan una gran variabilidad.
4. Se puede aplicar cuando se estratifique previamente la población o cuando se realice la fiscalización en dos o más períodos (por ejemplo cuando se realiza una fiscalización previa en fase interina o antes de los cierres de cuentas).

A continuación se describe el proceso a seguir cuando se aplica el enfoque estándar del MUM.

2.1- Tamaño de la muestra

Fórmula 1. Tamaño de la muestra MUM estandard

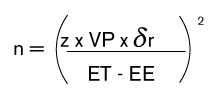
El primer paso será determinar el tamaño de la muestra a partir del cociente entre el valor de la población corregido y el gap de los errores (véase la fórmula 1):

Dónde:

• n es el tamaño de la muestra.
• z es el coeficiente de la distribución Normal.
• VP es el valor monetario de la población objeto de muestreo.
• _δr es la desviación estándar de los errores de la población.
• ET es el error tolerable máximo determinado en la fase de planificación de la fiscalización.
  EE es el error esperado por el auditor de acuerdo con su juicio profesional y la información previa. Este error ha de ser inferior al error tolerable (ET).

El valor de z dependerá del nivel de confianza exigido en la fiscalización después del análisis de los diferentes riesgos de auditoría. Este valor se puede determinar con tablas estadísticas o bien mediante fórmula en una hoja de cálculo^[2].

Como en general no se dispone de valores de la población actual, para obtener la desviación estándar de la población ϖ_r hay dos opciones:

1. Recurrir al valor obtenido en la auditoria de ejercicios anteriores.
2. Realizar una muestra aleatoria preliminar o muestra piloto de menor tamaño. En el caso de realizar previamente una muestra piloto se tendrá en cuenta que ésta será de entre 20 y 30 elementos. Esta muestra puede ser utilizada posteriormente como parte de la muestra seleccionada.

2.2- Selección de la muestra

Una vez establecido el tamaño de la muestra (n) el siguiente paso es segmentar los elementos de la población en dos estratos:

1. Estrato exhaustivo cuyos elementos formarán parte de la muestra y
2. Estrato no exhaustivo del que se seleccionarán aquellos elementos necesarios hasta alcanzar el tamaño de la muestra.

Para determinar el estrato exhaustivo deberá identificarse el importe a partir del cual todos los valores de la población serán seleccionados. Para obtener este importe se dividirá el valor de la población (VP) entre el tamaño de la muestra establecido (n). Todos los elementos de la población cuyo valor sea superior al valor de corte formarán parte del estrato exhaustivo y, por lo tanto, de la muestra (VPi > VP / n).

Para establecer el estrato no exhaustivo se separan de la población todos los elementos del estrato exhaustivo. A continuación se seleccionarán del estrato no exhaustivo los elementos necesarios para alcanzar el tamaño de la muestra establecido. Los elementos del estrato no exhaustivo serán seleccionados sistemáticamente  mediante un intervalo de muestreo (IM).

El proceso que sigue la selección de elementos del estrato no exhaustivo es el siguiente:

1. Se asigna a cada elemento del estrato un valor acumulativo de importes (por ejemplo el valor del tercer elemento será el valor acumulado del segundo más el suyo). Es importante que el estrato no
2. esté ordenado por los importes. Es recomendable ordenar aleatoriamente los elementos del estrato.
3. Se toma un valor inicial aleatorio para garantizar que todos tengan una probabilidad de salir. En caso contrario, los primeros no saldrían nunca si tuvieran un valor inferior al intervalo.
4. Se suma el valor inicial aleatorio con el IM y se selecciona el valor acumulado que contenga el importe de esa suma. Y así sucesivamente hasta alcanzar el tamaño de la muestra requerido. Cabe la opción de escoger como primer elemento que contenga el valor inicial aleatorio.

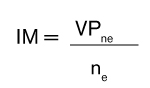
El intervalo de muestreo (IM) se calcula dividiendo el valor monetario total del estrato no exhaustivo (VPne) por el número de elementos a seleccionar (ne) (véase la fórmula 2).
Fórmula 2. Intervalo de muestreo

2.3 Fiscalización de la muestra

Una vez seleccionada la muestra, se fiscalizan los elementos seleccionados para detectar si existen errores y poder determinar el error de muestreo. Como ya se ha dicho anteriormente en este método únicamente se tienen en cuenta los errores por sobrevaloración.

2.4. Proyección de los errores

El objetivo final cuando se aplica un método de muestreo es proyectar el error detectado en la muestra al conjunto de la población para determinar si la población presenta errores materiales o no. La proyección de los errores en el MUM se realizará diferenciando el estrato exhaustivo y el estrato no exhaustivo.
Fórmula 3. Error proyectado estrato exhaustivo
El error proyectado en el estrato exhaustivo (EPee) se calcula sumando todos los errores encontrados en el estrato (véase la fórmula 3).

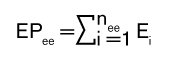
El error proyectado en el estrato no exhaustivo (EPne) se calculará de la siguiente manera:

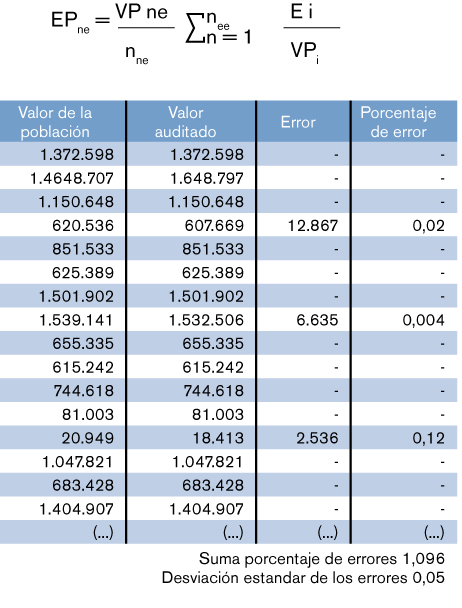
Fórmula 4. Tasa de error

1. Para cada elemento de la muestra se calculará la tasa de error dividiendo el error de cada elemento por su valor (Véase la fórmula 4).
2. Se sumarán todos las tasas de error obtenidos.
3. Se multiplica la suma de todos los ratios de error por el valor de la población del estrato no exhaustivo (VPne).
4. El resultado anterior se dividirá por el tamaño de la muestra del estrato no exhaustivo (nne) (Veáse la fórmula 5).

Fórmula 5. Error no proyectado, estrado no exhaustivo

El error proyectado total (EP) se obtendrá sumando los errores proyectados de los estratos exhaustivo y no exhaustivo (véase la fórmula 6).
Fórmula 6. Error  proyectado total

2.5. Precisión

La precisión es un concepto asociado al error de muestreo que mide e intenta corregir la incertidumbre asociada a la proyección de los errores. La precisión en el MUM estándar se calcula aplicando la siguiente fórmula:
Fórmula 8. Error  proyectado total

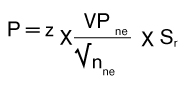
Dónde:

• z es el coeficiente de la distribución Normal asociado al nivel de confianza establecido por el auditor al analizar los riesgos de la auditoria.
• VPne es el valor de la población correspondiente al estrato no exhaustivo, puesto que es en este estrato en el que se realiza la extrapolación de errores.
• nne es el número de elementos de la muestra que pertenecen al intervalo no exhaustivo.
• Sr es la desviación estándar de los porcentajes de error de la muestra del estrato no exhaustivo.

2.6. Evaluación

Para concluir si los errores en la población son materiales  se debe determinar el límite superior del error (LSE) que se calcula sumando el error proyectado total (EP) y la precisión resultante de la extrapolación (P) (véase la fórmula 9).
Fórmula 9. Límite superior de error

A continuación tanto el error proyectado (EP) como el límite superior del error (LSE) deben compararse con el error tolerable^[3] (ET).  De esta comparación se pueden presentar tres situaciones posibles:

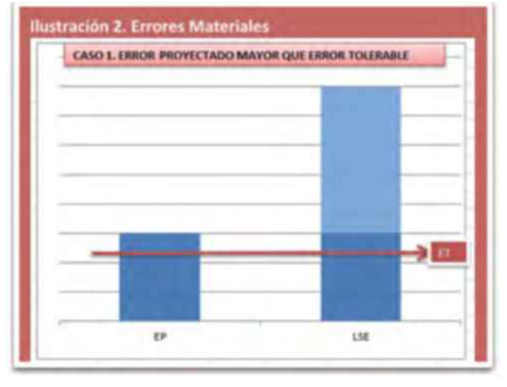
• Si el error proyectado (EP) es mayor que el error tolerable (ET), se concluirá que existe suficiente evidencia para soportar que la población presenta errores materiales (véase ilustración 2).
  
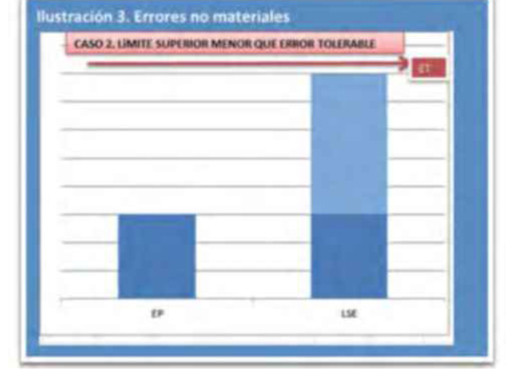
• Si el límite superior del error (LSE) es inferior al error tolerable (ET), se concluirá que lo errores existentes en la población no son materiales (véase ilustración 3).

• Si el error proyectado (EP) es inferior al error tolerable (ET) pero el límite superior del error (LSE) es superior al error tolerable (ET) se concluirá que no existe suficiente evidencia que soporte que no existen errores materiales en la población. Para llegar a una conclusión será necesario la realización de trabajo adicional (véase ilustración 4).

De acuerdo con la ISSAI 1530 de la INTOSAI el trabajo adicional podría consistir en:

• Solicitar a la entidad auditada investigar tanto los errores encontrados como la existencia de errores potenciales y realizar los ajustes necesarios.
• Aplicar procedimientos de auditoria adicionales para obtener la seguridad adicional requerida.

Para una mayor consolidación de conceptos, a continuación se desarrollará un caso práctico del enfoque estándar del MUM.

3. CASO PRÁCTICO

Datos iniciales

En una fiscalización de certificación de unos fondos agrícolas se disponen de los siguientes datos:

Se pide determinar el tamaño de la muestra a fiscalizar

Solución 1

Para establecer el tamaño de la muestra se utiliza la fórmula 1:

• El error tolerable de la población: 2% x 256.163.589 = 5.123.272;
• El error esperado: 20% x 5.123.272 = 1.024.654;
• Para un nivel de confianza del 90%, el parámetro de la distribución normal es de 1,64^[4].

Luego el tamaño de la muestra representado como como:

Una vez fijado el tamaño de la muestra se identificarán aquellos elementos de la población que por su mayor valor serán seleccionados y formarán parte del estrato exhaustivo. El valor de corte vendrá establecido por el ratio entre el valor total de la población (VP) y el tamaño de la muestra (n). Todos aquellos elementos cuyo valor supere el valor de corte serán seleccionados.

Datos complementarios

Disponemos de los siguientes datos complementarios, posteriores a la selección de la muestra:

• Se han detectado un total de 8 elementos que superan el valor de corte por un valor acumulado de 47.991.589.
• Una vez analizadas las operaciones seleccionadas en la muestra se han detectado los siguientes errores:
  
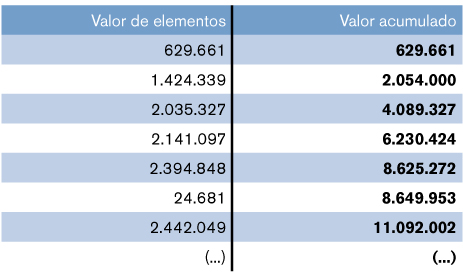
• Suponiendo que hemos determinado un valor inicial aleatorio de 2.592.772 y los 7 primeros elementos de la población son los siguientes:

• Y en la revisión de la muestra del estrato no exhaustivo se detecta que la desviación estándar de los errores es de 0,05 y la suma de los porcentajes de error es de 1,096.

Se pide determinar:

1. Los elementos de cada estrato (exhaustivo y no exhaustivo) que formarán parte de la muestra.
2. Determinar el intervalo de muestreo.
3. Seleccionar los 3 primeros elementos de la muestra.
4. Proyectar los errores y valorar los resultados obtenidos

Solución 2

Elementos de cada estrato
En relación con el estrato exhaustivo, los 8 elementos que superan el corte formarán parte de la muestra. Por consiguiente, se seleccionarán 68 elementos del estrato no exhaustivo para completar la muestra (76-8).

Intervalo de muestreo
Para seleccionar la muestra de los elementos del estrato no exhaustivo debe establecerse el intervalo de muestreo a partir del ratio entre el valor de la población del estrato no exhaustivo (el valor de la población menos el valor de los elementos del estrato exhaustivo)  y los elementos del estrato no exhaustivo.

Selección de la muestra en el estrato no exhaustivo

La muestra del estrato no exhaustivo se realizará ordenando aleatoriamente los elementos y seleccionando aquellos elementos que contengan el intervalo de muestreo (3.061.353).

Para realizar la selección se generará una tabla con las 2.756 operaciones del intervalo no exhaustivo (2.764-8 operaciones del estrato exhaustivo).

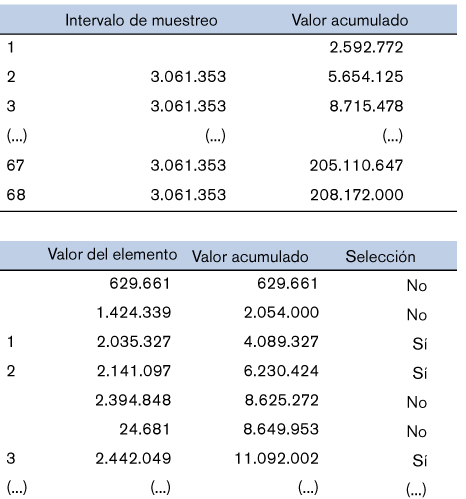
El primer elemento de la tabla seleccionado será el que tenga un valor acumulado igual o superior a 2.592.772, que es el número aleatorio seleccionado inicial, comprendido entre el intervalo cero y el intervalo de muestreo.

El segundo elemento seleccionado será aquel que acumule un valor de 5.654.125 (2.592.772+3.061.353). El tercer elemento seleccionado será aquel que acumule un valor de 8.715.478 (5.654.125+3.061.353) y así sucesivamente hasta seleccionar 68 elementos.

Proyección de errores
Para proyectar los errores detectados en la muestra al conjunto de la población deben proyectarse los errores del estrato no exhaustivo de la siguiente manera:

• Calculando el porcentaje de error de cada elemento.
  

• Sumando todos los porcentajes de error obtenidos.
• Multiplicando el resultado anterior por el intervalo de muestreo del estrato no exhaustivo.

El error proyectado total será la suma de los errores detectado en las 3 operaciones del estrato exhaustivo (464.572) más el error proyectado del estrato no exhaustivo:

Cálculo de la Precisión
El cálculo de la precisión (P) se realizará de la siguiente manera:

Evaluación

Para poder llegar a una conclusión sobre la materialidad de los errores debe calcularse el límite superior del error (LSE) que se obtiene sumando el error proyectado y la precisión de la extrapolación.

Como se deduce estamos ante la situación de la ilustración 4, ya que el error tolerable (5.123.272) es mayor que el error proyectado (3.819.815) pero menor que el límite superior del error (6.406.374). Por consiguiente, para poder concluir si la población contiene errores materiales será necesario realizar procedimientos de auditoría adicionales.

4. Conclusiones

El método estadístico de unidad monetaria (MUM), enfoque estándar resulta aplicable cuando se espera que en las poblaciones auditadas exista una sobrestimación del error.

La aplicación del enfoque estándar del MUM requiere del conocimiento de la desviación estándar de los errores en la población que podrá obtenerse del muestreo realizado en ejercicios anteriores o por una muestra piloto que permita estimar dicha desviación.

El MUM estándar es, en general, más complejo que el conservador pero permite seleccionar un tamaño de las muestras más pequeño.

Bibliografía
Australian National Audit Office. (1990): Audit sampling. Supplementary Audit Guide.
Comisión Europea. (2015): Directriz número 2 para la auditoria de certificación de las cuentas del FEAGA / FEADER relativa a la auditoria de la certificación anual.
Comisión Europea. (2013): Guía de métodos de muestreo para las autoridades de auditoria.
Francisco Julián Chico Martínez. (2007): Muestreo aleatorio en Auditoría. Revista Auditoría Pública nº 42.
Instituto de Censores Jurados de Cuentas de España. (2014): Cuaderno técnico número 21. Conceptos básicos de muestreo.

[1] Véase por ejemplo la Directriz número 2 de la Comisión Europea para la auditoria de certificación de las cuentas del FEAGA/FEADER relativa a la auditoria de la certificación anual.
[2] En Excel se calcula mediante la fórmula: =INV.NORM.ESTAND(1-((1-Co)/2)); donde Co es el valor del nivel de confianza en tanto por uno.
[3] El error tolerable es el error máximo aceptable que puede encontrarse en la población.
[4] En el enfoque estándar del MUM el valor z de la distribución Normal asociado al nivel de confianza establecido incluye la cola inferior de la distribución Normal. Para un nivel de confianza establecido del 90%, el valor z de la distribución estándar que incluye la cola inferior es de 1,64 que es el correspondiente al 95% (90%+5%).